CARBON NANOTUBES

Discovery of Carbon Nanotube

Sumio Iijima (born May 2, 1939) is a Japanese physicist, often cited as the discoverer of carbon nanotubes. In 1991 he observed Multiwalled carbon Nanotube and in 1993 he discovers Single wall carbon Nanotube. For this and other work Sumio Iijima was awarded, together with Louis Brus, the inaugural Kavli Prize for Nanoscience in 2008.

Introduction

Carbon nanotubes (CNTs) also called buckytubes are allotropes of carbon with a cylindrical nanostructure.

Basic Structure:

A single layer of graphite is called graphene and has extraordinary electrical, thermal, and physical properties.

Carbon nanotube (CNT) is a new form of carbon, configurationally equivalent to two dimensional graphene sheet rolled into a tube.The ends of a nanotube might be capped with a hemisphere of the buckyball structure. It is just a few nanometers in diameter and several microns long.They are light, flexible, thermally stable, and are chemically inert. They have the ability to be either metallic or semi-conducting depending on the "twist" of the tube.

Nanotubes are categorized as single-walled nanotubes (SWNTs) and multi-walled nanotubes (MWNTs).

Single-walled Nanotube (SWNTs)

It is equivalent to two dimensional graphene sheet rolled into a tube. Single-walled Nanotube can be considered as one-dimensional quantum wire.

Types of SWNTs

Nanotubes form different types, which can be described by the chiral vector (n, m), where n and m are integers of the vector equation R = na₁ + ma₂. The chiral vector is determined by the diagram below.

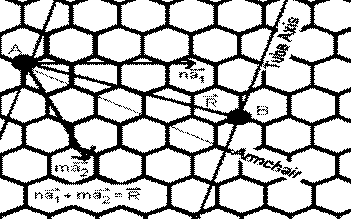
Imagine that the nanotube is unraveled into a planar sheet. Draw two lines along the tube axis where the separation takes place. In other words, if you cut along the two lines and then match their ends together in a cylinder, you get the nanotube that you started with. Now, find any point on one of the lines that intersects one of the carbon atoms (point A). Next, draw the Armchair line, which travels across each hexagon, separating them into two equal halves. Now that you have the armchair line drawn, find a point along the other tube axis that intersects a carbon atom nearest to the Armchair line (point B). Now connect A and B with our chiral vector, R.The wrapping angle ф, is formed between R and the Armchair line. If R lies along the Armchair line (ф=0°), then it is called an "Armchair" nanotube. If ф =30°, then the tube is of the "zigzag" type. Otherwise, if 0°< ф <30° then it is a "chiral" tube. The vector a₁ lies along the "zigzag" line.The other vector a₂ has a different magnitude than a₁, but its direction is a reflection of a₁ over the Armchair line. When added together, they equal the chiral vector R.

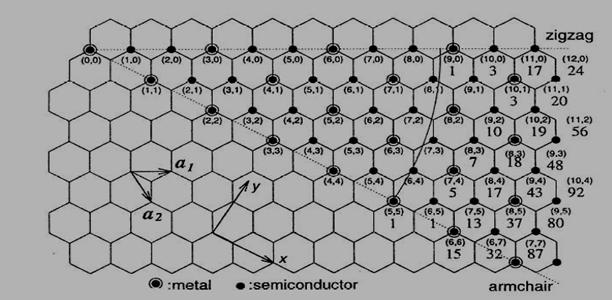
The values of n and m determine the chirality, or "twist" of the nanotube. The chirality in turn affects the conductance of the nanotube, its density, its lattice structure, and other properties.A SWNT is considered metallic if the value n - m is divisible by three or zero. Otherwise, the nanotube is semiconducting. Consequently, when tubes are formed with random values of n and m, we would expect that two-thirds of nanotubes would be semi-conducting, while the other third would be metallic. Another important parameter is the chiral angle, which is the angle between R and â₁.Given the chiral vector (n, m), the diameter of a carbon nanotube can be determined using the relationship

d = (n² + m² + nm) ^1/2 0.0783 nm

Chiral angle = tan^-1(Ö3n/(2m + n)).

Ropes of Carbon Nanotubes

In 1996, Thess et al. measured the properties of "ropes" of carbon nanotubes. As shown in the diagram at right, ropes are bundles of tubes packed together in an orderly manner. They found that the individual SWNTs packed into a close-packed triangular lattice with a lattice constant of about 17 Å. As a good estimate,the lattice parameter in CNT ropes (bundled nanotubes) is d + 0.34 nm, where d is the tube diameter given above.

Multiwalled Carbon nanotubes

Multi-walled nanotubes (MWNT) consist of multiple rolled layers (concentric tubes) of graphite. There are two models which can be used to describe the structures of multi-walled nanotubes.

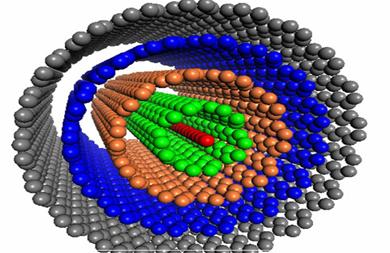
In the Russian Doll model, sheets of graphite are arranged in concentric cylinders, e.g. a (0, 8) single-walled nanotube (SWNT) within a larger (0, 10) single-walled nanotube. In the Parchment model, a single sheet of graphite is rolled in around itself, resembling a scroll of parchment or a rolled newspaper. The interlayer distance in multi-walled nanotubes is close to the distance between graphene layers in graphite, approximately 3.4 Å.

Properties Of CNT:

Physical Properties:

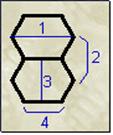
Average Diameter of SWNT	1.2-1.4 nm
Distance from opposite carbon atoms (Line 1)	2.83 A
Analogous Carbob atom separation(line 2)	2.456 A
Parallel carbon bond separation(line 3)	2.45 A
Carbon bond length(line4)	1.42 A
C – C tight bonding overlap energy	~ 2.5 ev
Lattice constant	17 A
Density (10,10) Armchair (17,0) Zigzag (12,6) Chiral	1.33 g/cm^3 1.34 g/cm^3 1.40 g/cm^3
Interlayer Spacing (n,n) Armchair (n,0) Zigzag (2n,n) Chiral	3.38 Å 3.41Å 3.39 Å

Optical Properties:

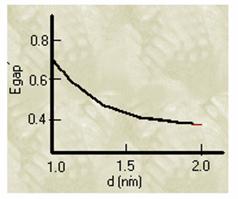
Fundamental Gap:

For (n, m); n-m is divisible by 3 [Metallic] 0 eV
For (n, m); n-m is not divisible by 3 [Semi-Conducting] ~ 0.5 eV

The fundamental gap (HOMO-LUMO) of semiconductor was a function of diameter ,where gap was in the order of about of 0.5eV.

E_gap=2y₀a_cc/d

Where y_{0 is} the C-C tight bonding overlap energy (2.70.1 eV), a_cc is the nearest distance (0.142nm),and d is the diameter.

Density of states:

Calculating the density of states for small structures shows that the distribution of electrons changes as dimensionality is reduced. For quantum wires, the DOS for certain energies actually becomes higher than the DOS for bulk semiconductors, and for quantum dots the electrons become quantized to certain energies.

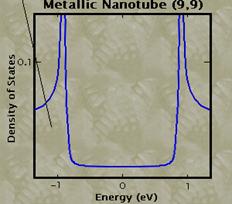
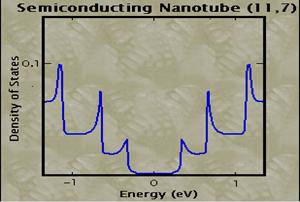
At the Fermi Energy (the highest occupied energy level), the density of states finite for a metallic tube (though very small), and zero for a semi-conducting tube. As energy is increased, sharp peaks in the density of states, called Van Hove singularities, appear at specific energy levels.

Electrical Properties:

Resistance 6500 Ω

Maximum Current Density 10¹³ A/m²

Thermal Properties:

Thermal Conductivity ~2000 W /m-K

Phonon Mean Free Path ~ 100 nm

Relaxation Time ~ 10^-11 s

Elastic Properties:

Young's Modulus (SWNT) ~ 1 Tpa

Young's Modulus (MWNT) 1.28 Tpa

Maximum Tensile Strength ~30 Gpa

Electronic Properties of Nanotubes:

The unique electronic properties of carbon nanotubes are due to the quantum confinement of

electrons normal to the nanotube axis. In the radial direction, electrons are confined by the monolayer thickness of the graphene sheet. Around the circumference of the nanotube, periodic boundary conditions come into play. For example, if a zigzag or armchair nanotube has 10 hexagons around its circumference, the 11th hexagonal will coincide with the first. Going around the cylinder once introduces a phase difference of 2∏.Because of this quantum confinement, electrons can only propagate along the nanotube axis, and so their wavevectors point in this direction. These simple ideas can be used to calculate the dispersion relations of the one-dimensional bands, which link wavevector to energy, from the well known dispersion relation in a graphene sheet.

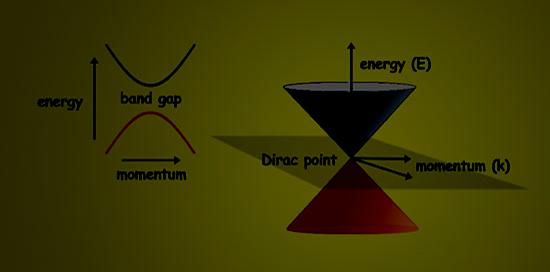
Although the choice of n and m determines whether the nanotube is metallic or semiconducting, the chemical bonding between the carbon atoms is exactly the same in both cases. This Surprising result is due to the very special electronic structure of a two-dimensional graphene sheet, which is a semiconductor with a zero band gap. In this case, the top of the valence band has the same energy as the bottom of the conduction band, and this energy equals the Fermi energy for one special wavevector, the so-called K-point of the two-dimensional Brillouin zone (i.e. the corner point of the hexagonal unit cell in reciprocal space). Theory shows that a nanotube becomes metallic when one of the few allowed wavevectors in the circumferential direction passes through this K-point. As the nanotube diameter increases, more wavevectors are allowed in the circumferential direction. Since the band gap in semiconducting nanotubes is inversely proportional to the tube diameter, the band gap approaches zero at large diameters, just as for a graphene sheet. At a nanotube diameter of about 3 nm, the band gap becomes comparable to thermal energies at room temperature. The concentric pairs of metal-semiconductor and semiconductor-metal nanotubes are stable. Nanometre-scale devices could therefore be based on two concentric nanotubes or the junction between nanotubes. For example, a metallic inner tube surrounded by a larger semiconducting (or insulating) nanotube would form a shielded cable at the nanometre scale. Unlike electrons in other materials, the electrons in graphene move ballistically — without collisions — over great distances, even at room temperature. As a result, the ability of the electrons in graphene to conduct electrical current is 10 to 100 times greater than those in a normal semiconductor like silicon at room temperature.

Synthesis of Carbon Nanotube

Arc Method:

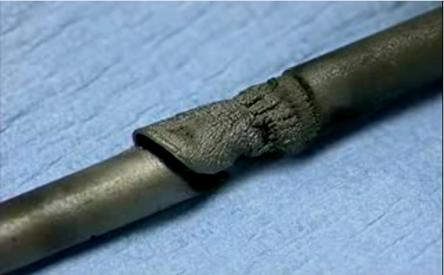
The carbon arc discharge method is the most common and perhaps easiest way to produce CNTs, as it is rather simple. However, it is a technique that produces a complex mixture of components, and requires further purification - to separate the CNTs from the soot and the residual catalytic metals present in the crude product.  This method creates CNTs through arc-vaporization of two carbon rods placed end to end, separated by approximately 1mm, in an enclosure that is usually filled with inert gas at low pressure. Recent investigations have shown that it is also possible to create CNTs with the arc method in liquid nitrogen. A direct current of 50 to 100A, driven by a potential difference of approximately 20 V, creates a high temperature discharge between the two electrodes. The discharge vaporizes the surface of one of the carbon electrodes, and forms a small rod-shaped deposit on the other electrode. Producing CNTs in high yield depends on the uniformity of the plasma arc, and the temperature of the deposit forming on the carbon electrode. The yield for this method is up to 30 percent by weight and it produces both single- and multi-walled nanotubes with lengths of up to 50 micrometers with few structural defects.

Laser ablation:

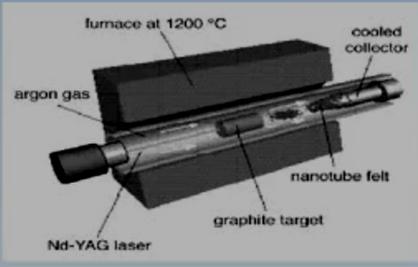
This process was developed by Dr. Richard Smalley and co-workers at Rice University

In 1996 CNTs were first synthesized using a dual-pulsed laser and achieved yields of >70wt% purity. Samples were prepared by laser vaporization of graphite rods with a 50:50 catalyst mixture of Cobalt and Nickel at 1200°C in flowing argon, followed by heat treatment in a vacuum at 1000°C to remove the C60 and other fullerenes. The initial laser vaporization pulse was followed by a second pulse, to vaporize the target more uniformly. The use of two successive laser pulses minimizes the amount of carbon deposited as soot. The second laser pulse breaks up the larger particles ablated by the first one, and feeds them into the growing nanotube structure. The material produced by this method appears as a mat of "ropes", 10-20nm in diameter and up to 100µm or more in length. Each rope is found to consist primarily of a bundle of single walled nanotubes, aligned along a common axis. By varying the growth temperature, the catalyst composition, and other process parameters, the average nanotube diameter and size distribution can be varied. The laser ablation method yields around 70% and produces primarily single-walled carbon nanotubes with a controllable diameter determined by the reaction temperature. However, it is more expensive than either arc discharge or chemical vapor deposition. Arc-discharge and laser vaporization are currently the principal methods for obtaining small quantities of high quality CNTs. However, both methods suffer from drawbacks. The first is that both methods involve evaporating the carbon source, so it has been unclear how to scale up production to the industrial level using these approaches. The second issue relates to the fact that vaporization methods grow CNTs in highly tangled forms, mixed with unwanted forms of carbon and/or metal species. The CNTs thus produced are difficult to purify, manipulate, and assemble for building nanotube-device architectures for practical applications.

Chemical Vapour Deposition:

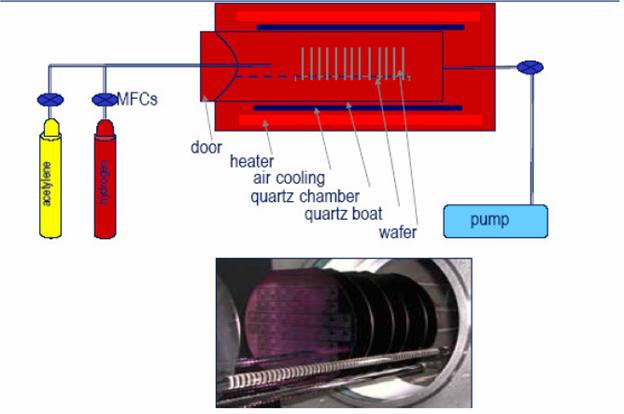
During CVD, a substrate is prepared with a layer of metal catalyst particles, most commonly nickel, cobalt, iron, or a combination. The metal nanoparticles can also be produced by other ways, including reduction of oxides or oxides solid solutions. The diameters of the nanotubes that are to be grown are related to the size of the metal particles. This can be controlled by patterned (or masked) deposition of the metal, annealing, or by plasma etching of a metal layer. The substrate is heated to approximately 700°C. To initiate the growth of nanotubes, two gases are bled into the reactor: a process gas (such as ammonia, nitrogen or hydrogen) and a carbon-containing gas (such as acetylene, ethylene, ethanol or methane). Nanotubes grow at the sites of the metal catalyst; the carbon-containing gas is broken apart at the surface of the catalyst particle, and the carbon is transported to the edges of the particle, where it forms the nanotubes. This mechanism is still being studied. The catalyst particles can stay at the tips of the growing nanotube during the growth process, or remain at the nanotube base, depending on the adhesion between the catalyst particle and the substrate.

If a plasma is generated by the application of a strong electric field during the growth process (plasma enhanced chemical vapor deposition*), then the nanotube growth will follow the direction of the electric field. By adjusting the geometry of the reactor it is possible to synthesize vertically aligned carbon nanotubes (i.e., perpendicular to the substrate), a morphology that has been of interest to researchers interested in the electron emission from nanotubes. Without the plasma, the resulting nanotubes are often randomly oriented. Under certain reaction conditions, even in the absence of plasma, closely spaced nanotubes will maintain a vertical growth direction resulting in a dense array of tubes resembling a carpet or forest.

Advantages of Multi-walled Nanotube:

The special place of double-walled carbon nanotubes (DWNT) must be emphasized here because their morphology and properties are similar to SWNT but their resistance to chemicals is significantly improved. This is especially important when functionalization is required (this means grafting of chemical functions at the surface of the nanotubes) to add new properties to the CNT. In the case of SWNT, covalent functionalization will break some C=C double bonds, leaving "holes" in the structure on the nanotube and thus modifying both its mechanical and electrical properties. In the case of DWNT, only the outer wall is modified. While multi-wall carbon nanotubes do not need a catalyst for growth, single-wall nanotubes can only be grown with a catalyst. Their larger diameter favours low-ohmic contacts, they do not contain magnetic impurities, they have very well ordered structure, high conductivity and their mesoscopic size enables the observation of quantum interference effects like the Aharonov-Bohm effect. The latter magnetotransport measurements can all very well be understood.

Advantages of Single-walled Nanotube:

The results from multi-wall nanotubes are complicated by simultaneous contributions fromconcentric nanotubes with different diameters and chiralities. In addition, defects in the multiwalled nanotubes can lead to electron scattering and electrical contact cannot be made reliably to all of the constituent nanotubes. The conduction properties of the electrical contacts can also influence electron transport. Further experimental studies of these intriguing transport phenomena should be made on smaller diameter multi-wall nanotubes and at low temperatures, where one-dimensional quantum effects can be observed. The situation in multi-wall CNTs is complicated as their properties are determined by contribution of all individual shells; those shells have different structures, and, because of the synthesis, are usually more defective than SWCNTs.

Applications

Field Emission:

Buckytubes are the best known field emitters. This is understandable, given their high electrical conductivity, and the unbeatable sharpness of their tip (the sharper the tip, the more concentrated will be an electric field, leading to field emission; this is the same reason lightening rods are sharp). The sharpness of the tip also means that they emit at especially low voltage, an important fact for building electrical devices that utilize this feature. Buckytubes can carry an astonishingly high current density, possibly as high as 10¹³ A/cm². Furthermore, the current is extremely stable. An immediate application of this behaviour receiving considerable interest is in field-emission flat-panel displays. Instead of a single electron gun, as in a traditional cathode ray tube display, here there is a separate electron gun (or many) for each pixel in the display. The high current density, low turn-on and operating voltage, and steady, long-lived behaviour make buckytubes attract field emitters to enable this application.

Molecular Electronics:

The idea of building electronic circuits out of the essential building blocks of materials - molecules - has seen a revival the past five years, and is a key component of nanotechnology. In any electronic circuit, but particularly as dimensions shrink to the nanoscale, the interconnections between switches and other active devices become increasingly important.

Their geometry, electrical conductivity, and ability to be precisely derived, make buckytubes the ideal candidates for the connections in molecular electronics. In addition, they have been demonstrated as switches themselves.

Conductive Plastics:

Much of the history of plastics over the last half century has been as a replacement for metal. For structural applications, plastics have made tremendous headway, but not where electrical conductivity is required, a plastic being famously good electrical insulators.This deficiency is overcome by loading plastics up with conductive fillers, such as carbon black and graphite fibres (the larger ones used to make golf clubs and tennis racquets). The loading required to provide the necessary conductivity is typically high, however, resulting in heavy parts, and more importantly, plastic parts whose structural properties are highly degraded.It is well established that the higher aspect ratio of filler, the lower loading required to achieve a given level of conductivity. Buckytubes are ideal in this sense, since they have the highest aspect ratio of any carbon fibre. In addition, their natural tendency to form ropes provides inherently very long conductive pathways even at ultra-low loadings.

Applications that exploit this behaviour of buckytubes include EMI/RFI shielding composites and coatings for enclosures, gaskets, and other uses; electrostatic dissipation (ESD), and antistatic materials and (even transparent!) coatings; and radar-absorbing materials.

Energy Storage:

Buckytubes have the intrinsic characteristics desired in material used as electrodes in batteries and capacitors, two technologies of rapidly increasing importance. Buckytubes have a tremendously high surface area (~1000 m²/g), good electrical conductivity, and very importantly, their linear geometry makes their surface highly accessible to the electrolyte.

Research has shown that buckytubes have the highest reversible capacity of any carbon material for use in lithium-ion batteries. In addition, buckytubes are outstanding materials for supercapacitor electrodes and are now being marketed.

Catalyst Supports

Buckytubes have an intrinsically high surface area; in fact, every atom is not just on a surface - each atom is on two surfaces, the inside and outside! Combined with the ability to attach essentially any chemical species to their sidewalls provides an opportunity for unique catalyst supports. Their electrical conductivity may also be exploited in the search for new catalysts and catalytic behaviour.

Biomedical Applications:

The ability to chemically modify the sidewalls of buckytubes also leads to biomedical applications such as vascular stents, and neuron growth and regeneration.

Fibres and Fabrics:

Fibres spun of pure buckytubes have recently been demonstrated and are undergoing rapid development, along with buckytube composite fibres. Such super strong fibres will have applications including body and vehicle armour, transmission line cables, woven fabrics and textiles.